我的学习笔记

# 数论（一）

# 1.同余系统

# 1.1 最大公约数(Greatest common divisor (opens new window))

# 1.1.1 表示x和y的最大公约数，也叫最大公因数，例如

欧几里得对“公约”的解释，给定两条长度不同的线段 a 和 b ，如果能够找到第三条线段 c ，它既可以度量 a ，又可以度量 b ，我们就说 a 和 b 是可公约的(commensurable)，最大可能的c就是a和b的最大公约数

# 1.1.2 如果两个数的最大公约数是1，那么这两个数成是互质的(relatively prime)，比如说

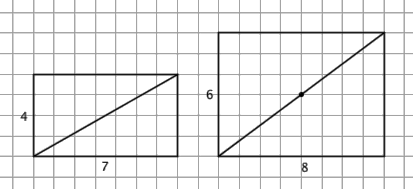
互质的几何意义，如果 a 和 b 互质，这就意味着分数 a / b 已经不能再约分了，意味着 a × b 的棋盘的对角线不会经过中间的任何交叉点，意味着循环长度分别为 a 和 b 的两个周期性事件一同上演，则新的循环长度最短为 a × b 。

# 1.1.3 最大公约数一般使用欧几里得碾压相除法(Euclidean algorithm (opens new window))计算

欧几里得算法使用了如下递归式

的计算方法

# 1.2 最小公倍数(Least Common Multiple (opens new window))

表示x和y的最小公倍数,例如

# 1.3 模运算

# 1.3.1 是x除以n的余数,例如

# 1.3.2 模运算符合交换律，结合律和分配律

# 1.3.3 如何计算

如果是2的幂次方，例如16，那么
如果不是2的幂次方，例如


# 1.4 同余等式

如果和除的余数相同，那么记为
如果，那么
如果，那么记为
如果，那么

# 2.中国剩余定理

# 2.1 孙子算经中的问题

“今有物，不知其数。三、三数之，剩二；五、五数之，剩三；七、七数之，剩二。问物几何？答曰：二十三。”
《孙子算经》卷下第二十六问

# 2.2 数学解释

有个两两互质的数，其乘积为，有一个未知数，如果我们已知分别除以这个数所得的余数，那么在0到的范围内，我们可以唯一地确定这个

# 2.3 直觉

两个除数的情况为例，假设两个除数分别是 4 和 7。下表显示的就是各自然数除以 4 和除以 7 的余数情况
0 1 2 3 0 1 2 3 0 1 2 3 0 1 2 3 0 1 2 3
0 1 2 3 4 5 6 0 1 2 3 4 5 6 0 1 2 3 4 5
0 1 2 3 0 1 2 3 0 1 2 3 0 1 2 3 0 1 2 3
6 0 1 2 3 4 5 6 0 1 2 3 4 5 6 0 1 2 3 4

可以看出，的结果以长度循环，每种特性的组合都在这28个结果中出现，所以一旦确定和的余数，就一定能唯一判定出

# 2.4 数学表达

已知是两两互质的正整数，有未知数满足同余方程组

那么

其中, 而是的逆元（见3.3节），也就是

# 2.5 举例，孙子算经中的问题

，那么

# 3.欧拉定理

# 3.1 欧拉函数

任意给定正整数，小于等于的正整数之中，与n构成互质关系的数的个数记为

如果是质数，那么，
如果
如果，那么

比如

# 3.2 欧拉定理

如果和互质，那么

# 3.2.1

，

# 3.2.2

，所以尾数一定是1

# 3.2.3

由于, 所以，所以尾数为9

# 3.3 模反元素（逆元）

如果和互质，那么有解，称为模的模反元素

# 3.3.1

用欧拉定理证明，所以都是a的模反元素

# 3.3.2

例如求解同余方程，那么，所以都是同余方程的解

# 3.4 费马小定理

根据欧拉定理，当是一个质数时，对于任意正整数，有，如果，那么

# 4.扩展碾压相除法

# 4.1 裴蜀定理

对于方程，当且仅当时，方程有整数解

# 4.2 算法实现

对于方程, 假设方程有整数解，由于,可以得到

所以

用递归算法实现

pair<int,int> exgcd(int a,int b){
    if(b == 0)return make_pair(1,0);
    pair<int,int>temp = exgcd(b,a%b);
    pair<int,int>ans = make_pair(temp.second,temp.first-(int)(a/b)*temp.second);
    return ans;
}

← 数论（二） →