# 环境光渲染(二）

# 3. 高光部分

# 3.1 原理

光照方程中的高光部分

同样使用蒙特卡洛进行近似积分

这种方法的好处是可以通过分开预计算，尽量减少实际渲染时的计算量，这个公式可以理解为“Env. lighting x BRDF”，左边的第一部分是小平面受到的所有环境光的采样值，第二部分只跟材质的BRDF属性相关。

# 3.2 预渲染环境光贴图（pre-filtered environment map)

第一个拆分项只和环境光照以及采样点有关，首先采样点集中在周围（是相对于法线的反射向量），并且粗糙度越大，采样点越分散。

实际应用中，这个拆分项是通过把环境光贴图预先渲染到一个环境贴图中实现的，称为为"pre-filter map"或者"radiance map"，最终渲染时根据，以及把粗糙度(0~1)转换为mip获得该方向的数值

# 3.3 预渲染贴图的生成

生成这张贴图时，首先假定，也就是摄像机从法线方向垂直观察小平面，然后开始采样

再最终渲染时，当和不等时，采样点的分布会有一定差异，但基本上可以忽略

# 3.3.1 采样点的生成

根据前面章节的分析，微表面的法线分布可以用法线分布函数描述，并且符合

由于微表面法线的概率密度函数符合以下公式

所以

用极坐标表示

对于各向同性系统，和无关，所以

D函数使用GGX函数，也就是

其中，此时

计算的概率分布函数

使用Mathmatica计算可得

根据前面的概率知识，可以得到微表面的法线的球坐标和的采样函数为

然后即可计算出光线采样点的入射向量

# 3.3.2 代码

实际运算时，每个采样点的权重是不一样的，采用和宏法线的点积作为权重

// make the simplyfying assumption that V equals R equals the normal 
vec3 R = N;
vec3 V = R;

const uint SAMPLE_COUNT = 1024u;
vec3 prefilteredColor = vec3_splat(0.0);
float totalWeight = 0.0;

for(uint i = 0u; i < SAMPLE_COUNT; ++i)
{
    // generates a sample vector that's biased towards the preferred alignment direction (importance sampling).
    vec2 Xi = Hammersley(i, SAMPLE_COUNT);
    vec3 H = ImportanceSampleGGX(Xi, N, roughness);
    vec3 L  = normalize(2.0 * dot(V, H) * H - V);

    float NdotL = max(dot(N, L), 0.0);
    if(NdotL > 0.0)
    {
        prefilteredColor += texture2D(s_texSkybox, SampleSphericalMap(L)).rgb * NdotL;
        totalWeight      += NdotL;
    }
}

prefilteredColor = prefilteredColor / totalWeight;

# 3.3 BRDF部分

观察公式的第二个拆分项

其中

设，那么

带入上面的式中，可得

设

那么可得

# 3.4 BRDF查找贴图

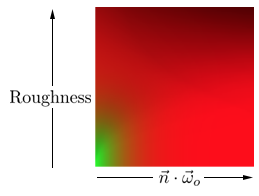
上面的公式中，除了和运行时的材质相关，其他数值都只取决于所使用的微表面的函数类型，所以可以预先计算在一张二维贴图中

在运行时可以使用查表得方式从这张贴图上获取数据

# 3.4.1 BRDF贴图的生成

vec2 IntegrateBRDF(float NdotV, float roughness)
{
    vec3 V;
    V.x = sqrt(1.0 - NdotV*NdotV);
    V.y = 0.0;
    V.z = NdotV;

    float A = 0.0;
    float B = 0.0; 

    vec3 N = vec3(0.0, 0.0, 1.0);
    
    const uint SAMPLE_COUNT = 1024u;
    for(uint i = 0u; i < SAMPLE_COUNT; ++i)
    {
        // generates a sample vector that's biased towards the
        // preferred alignment direction (importance sampling).
        vec2 Xi = Hammersley(i, SAMPLE_COUNT);
        vec3 H = ImportanceSampleGGX(Xi, N, roughness);
        vec3 L = normalize(2.0 * dot(V, H) * H - V);

        float NdotL = max(L.z, 0.0);
        float NdotH = max(H.z, 0.0);
        float VdotH = max(dot(V, H), 0.0);

        if(NdotL > 0.0)
        {
            float G = GeometrySmith(N, V, L, roughness);
            float G_Vis = (G * VdotH) / (NdotH * NdotV);
            float Fc = pow(1.0 - VdotH, 5.0);

            A += (1.0 - Fc) * G_Vis;
            B += Fc * G_Vis;
        }
    }
    A /= float(SAMPLE_COUNT);
    B /= float(SAMPLE_COUNT);
    return vec2(A, B);
}

← 环境光渲染(一) 环境搭建 →